Blinded Sample Size Re-estimation for Continuous Endpoints - Part 2

As noted in Part 1 of this series, the combined data from a two-group parallel study with a continuous endpoint can be viewed as a random sample from a two-component Gaussian mixture model with a known mixture proportion. Let 𝑋 denote an observation from the combined data, then

where 𝜔 is the mixture proportion, µ₁ and µ₂ are the component means, and σ² is the common variance. Let 𝛿 = µ₁ - µ₂ and 𝜔 = 1/2, then the variance of the mixture distribution is given by

Eq. (1) indicates that blinded sample size re-estimation (SSR) can be performed using the sample variance of the combined data when either σ² or 𝛿² is reliably obtained from historical studies. However, this reliance on historical information is a key limitation of this approach. The good news is that the (non-excess) kurtosis 𝜅 of the mixture distribution is

We can use Eq. (1) and Eq. (2) to solve for 𝛿² and σ², then obtain

Eq. (3) implies that the ratio 𝜆 = 𝛿²/σ² can be estimated by

where 𝜅̂ denotes the sample kurtosis of the pooled data. It's clear that this estimator is well defined only if 1 < 𝜅̂ ≤ 3, so it will be defined as zero if 𝜅̂ >3 (note that it is unlikely to observe 𝜅̂ ≤ 1 in practice).

Since the required sample size depends on 𝛿² and σ² only through the ratio 𝜆 = 𝛿²/σ², Eq. (4) suggests that blinded SSR can be performed using the pooled sample kurtosis, eliminating the need for historical estimates of either parameter. But how good is this estimator?

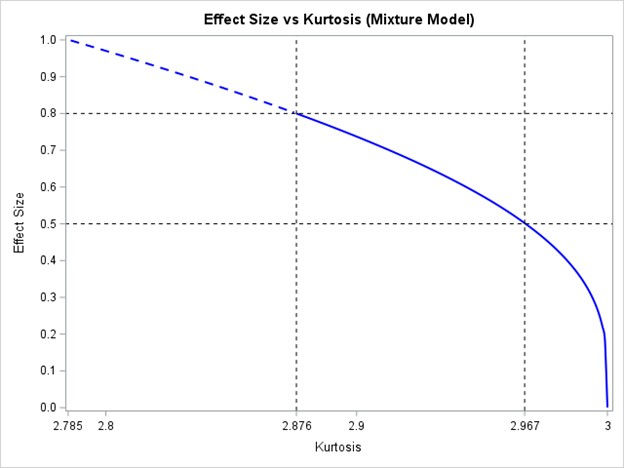
The graph below shows the effect size (𝛿/σ) in the range of [0, 1] as a function of the kurtosis (𝜅), where the solid curve represents the most likely scenarios in clinical trials. It is clear that the effect size is very sensitive to the changes in the kurtosis, which has a narrow range of 2.876 to 3 when 𝛿/σ ∊ [0, 0.8]. This suggests that a small bias in the estimate of 𝜅 can lead to a large bias in that of the effect size.

It can be shown that 𝜅̂ has asymptotic variance

where 𝑛 is the pooled sample size. Using the delta method, we have

where 𝜆'(𝜅) = -(𝜆+4)³/16𝜆 is the first order derivative of 𝜆 at 𝜅.

The following table reports the asymptotic variances Var(𝜅̂) and Var(𝜆^{^}) evaluated at different 𝜆 (and corresponding 𝛿/σ) values spanning a range commonly encountered in practice.

These results indicate that, despite its mathematical elegance, the estimator for 𝜆 in Eq. (4) is extremely unstable and therefore unsuitable for practical use.